Another way to accumulate data in vectors
From time to time, some #lisp-ers debate whether it’s faster to accumulate a
sequence of values using cons/nreverse, or cons/(setf cdr). To me, if that’s an
issue, you simply shouldn’t use a linked list; as Slava once wrote, “single linked lists
are simply the wrong data structure in 99% of cases.” A vector won’t be much or any
slower to build, and traversing a long vector is often far quicker than traversing an
equally long linked list, if only because the vector uses half as much space (and thus
memory bandwidth). The obvious question is then: how should we accumulate data
in vectors? (clearly, building a linked list and coercing it to a vector, as SBCL sometimes
does, isn’t ideal)
1 The simplest way
Obviously, the ideal way is to know the size of the final vector (or a reasonable overapproximation) ahead of time. The whole vector can then be preallocated, and, if needed, trimmed a posteriori. In terms of memory accesses, this pretty much achieves the lower bound of exactly one access per vector element. It’s also rarely applicable.
2 The usual way
The usual way to approach the problem of an unknown vector size is to begin with
an underapproximation of the final size, and grow the vector geometrically (and copy
from the old one) when needed. That’s the approach usually shown in textbooks, and
almost necessarily used by std::vector.
Unless the initial guess is very accurate (or too high), this method has a noticeable overhead in terms of memory access per vector element. Asymptotically, the best case is when the last grow is exactly the size of the final vector. For instance, when growing temporary vectors by powers of two, this happens when the final vector size is also a power of two. Then, in addition to the one write per element, half are copied once, a quarter once again, etc., for a total of ≈ 2 writes per element. The worst case is when the final vector has exactly one more element; for powers of two, all but one vector element are then copied once, half of that once again, etc., resulting in ≈ 3 writes per element.
C programs can often do much better by using realloc (or even mremap)
to avoid copies. High level languages can, in principle, do as well by also
hooking in the memory allocator. C++’s std::vector, however, can’t exploit
either: it must go through constructors and operator= (or std::swap, or
std::move). A variant of realloc that fails instead of moving the data could be
useful in those situations; I don’t know of allocators that provide such a
function.
3 A lazier way
Another way to build a vector incrementally is to postpone copying to a single contiguous vector until the very end. Instead, a sequence of geometrically larger temporary vectors can be accumulated, and only copied once to a final vector of exactly the right size. Since the temporary vectors grow geometrically, there aren’t too many of them (proportional to the logarithm of the final vector size), and the sequence can be represented simply, as a linked list, a flat preallocated vector, or a vector that’s copied when resized.
This yields, in all cases, exactly one write and one copy per element, and
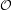 (lg n) bookkeeping operations for the sequence, for a total of ≈ 2 writes per
element.
(lg n) bookkeeping operations for the sequence, for a total of ≈ 2 writes per
element.
4 Testing the hypothesis
I used my trusty X5660 to test all three implementations, in C, when building a
vector of around 224unsigned elements (enough to overflow the caches). The table
below summarizes the results, in cycles per vector element (median value of 256).
The row for 224- 1 and 224 elements represent the best case for the usual growable
vector, 224 + 1 the worst case, and 224⋅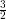 an intermediate value (usual case). The
relative values were similar with implementations in SBCL, both on a X5660 and on
a Core 2.
an intermediate value (usual case). The
relative values were similar with implementations in SBCL, both on a X5660 and on
a Core 2.
| size (n) | preallocate (c/n) | grow (c/n) | lazy (c/n) |
| 224- 1 | 7.52 | 13.39 | 15.01 |
| 224 | 7.55 | 13.39 | 15.29 |
| 224 + 1 | 7.55 | 19.63 | 13.91 |
224⋅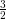 | 7.54 | 15.51 | 15.35 |
The numbers for preallocated vectors are reassuringly stable, at 7.5 cycles per vector element (2 cycles per byte). The usual way to grow a vector ends up using a bit less than twice as many cycles in the best cases, almost exactly twice in the usual case, and nearly three times as many cycles in the worst case. In contrast, lazy copying consistently uses twice as many cycles as the preallocated vector. These figures fit nicely with the theoretical cost in memory accesses. The main discrepancy is that growable vectors seem to do slightly better than expected for the best cases; this is probably due to the data caches, which significantly accelerate copying the first few temporary vectors.
5 Conclusion
The usual way to implement growable vectors has issues with performance on vectors
slightly longer than powers of two; depending on the computation:bandwidth cost
ratio, a task could become 50% slower when the number of outputs crosses a power of
two. Lazy copying, on the other hand, has very similar performance in most cases,
without the glass jaw around powers of two. The effect is even more important
when copying is more expensive, be it due to copy constructors, or to slower
implementations of memcpy (e.g. SBCL).
I’ve been working on a library for SERIES-style fusion of functional sequence operations, lately (in fact, that’s what lead me to benchmark lazy copying), and decided to spend the time needed to implement accumulation of values with lazily-copied vectors. The cost is mostly incurred by myself, while there isn’t any difference in the interface, and the user notices, at worst, a slight slowdown compared to the usual implementation. For instance,
(pipes (let ((x (from-vector x)))
(to-vector (remove-if-not (plusp x) x))))
will accumulate only the strictly positive values in x, without any unexpected major
slowdown around powers of two.
Growable vectors are often provided by (standard) libraries, and used by programmers without giving explicit thought to their implementation. Glass jaws should probably be avoided as much as possible in this situation, even at the cost of additional code off the hot path and a little pessimisation in the best cases.
