Paul Khuong mostly on Lisp

TL;DR: program-generated Common Lisp for a memory-bound task (FFT) can reach runtime performance identical to solid C code (djbfft), and close to the state of the art (FFTW).

Discrete fourier transforms are an interesting case study in high-performance computing: they’re extremely regular recursive computations, completely free of control dependencies, and memory-bound. The recursiveness and regularity means they can be expressed or generated with relatively little code, freedom of control dependency makes them easier to benchmark, and memory-boundedness ensures that low-level instruction-selection issues can mostly be ignored. Basically, they’re perfect for specialised compilers that generate Common Lisp code. With SBCL, we have decent control over how things are laid out in memory and reasonable compilation of high-level constructs like function calls or complex float multiplication; its simple colouring register allocator and naïve code generation sometimes yield nasty assembly, but the net effect is virtually noise compared to the memory latency inherent to the algorithms.

I pushed Napa-FFT on github last week. It’s an implementation of Bailey’s 6-step FFT [PDF] algorithm, which breaks DFTs of size n into 2 DFTs of size (with appropriate rounding up/down when n isn’t a perfect square). I found the 6-step algorithm interesting because it seems perfect to exploit caches. Reducing computation size by a factor of ≈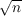 is huge: 1M complex doubles, which usually overflows L2 or even L3 caches, becomes 1K, and that fits comfortably in most L1 caches. This huge reduction also means that the algorithm has a very shallow recursion depth. For example, three recursion steps suffice to re-express a DFT of 16 M complex doubles as a (large) number of 8-point DFT base cases.

I completely failed to realize the latter characteristic, and I feel the approach taken in Napa-FFT is overly complex. This is where Napa-FFT2 comes in. It’s a complete rewrite of the same general idea, but explicitly structured to exploit the shallow recursion depth. This suffices to yield routines that perform comparably to djbfft on small or medium inputs, and only 25-50% slower than FFTW on large inputs.

1 Napa-FFT2

Napa-FFT2 features a small number of routine generators, each geared toward different input sizes. A first FFT generator handles small inputs and base cases for other routines; this family of routines is not expected to fare well on even medium inputs. A second generator is dedicated to slightly larger inputs and reduces medium FFTs to small ones, and a final generator builds upon the small and medium FFT generators to process even the largest inputs. Thus, there are at most two levels of recursion before specialised base cases are executed.

1.1 Radix-2 routine generator

The small FFT generator implements the same radix-2 approach as Bordeaux-FFT: tiny DFTs on indices in bit-reversed order, followed by lg n steps of contiguous additions or subtractions (butterflies) and multiplications by twiddle factors. Overall, it’s a very good algorithm: only the leaf DFTs aren’t on contiguous addresses, and the number of arithmetic operations is close to the best upper bounds known to date. The generator in Napa-FFT2 improves on Bordeaux-FFT by implementing larger base cases (up to n = 8), constant-folding most of the address computations and recognizing that no temporary vector is needed.

The only issue is that the access pattern needed to exploit the structure of the DFT matrix is awful on all but the smallest sizes. An L2 cache of 2 MB can only hold 128K complex doubles; for a lot of programs, temporal locality ensures most accesses hit cache even if the working set exceeds cache size. Unfortunately, the opposite happens with bit-reversed ordered accesses. The closest two indices are (e.g. they only differ in the least significant bit), the farther apart they are accessed, time-wise (see figure 1).

This explains the strong performance degradation in figure 2. The graph reports cycle counts on my 2.8 GHz X5660, which has (per core) 32 KB of L1D, 256 KB of L2, and 12 MB of L3 cache per socket. For tiny inputs, the constant overhead (function calls, the cpuid/rdtsc sequence, etc.) dominates, but, afterwards, we observe a fairly constant slope until 2¹², and then from 2¹³ to 2¹⁷; finally from 2¹⁸ onward, performance degrades significantly. This fits well with the cache sizes. If we take into account the input, output and twiddle factor vectors, the jump from 2¹² to 2¹³ overflows L2, and 2¹⁷ to 2¹⁸ L3.

1.2 2/4/6-step FFT algorithms

This is the effect that the 6-step algorithm attempts to alleviate. Each recursive FFT is significantly smaller: transforms of size 2¹⁸, which overflows L3, are executed as transforms of size 2⁹, which fits in L1. The total algorithmic complexity of the transform isn’t improved, but the locality of memory accesses is.

Gentleman and Sande describe how the DFT on a vector can be re-expressed as multiple DFTs on columns of row-major matrices, plus a transposition and an element-wise multiplication by a close cousin of the DFT matrix (figure 3). The transposition is nearly free of arithmetic, while the element-wise multiplication only involves streaming memory accesses, so fusing them makes a lot of sense.

The 6-step algorithm adds two transposition steps, before and after the four steps. This way, each sub-FFT operates on adjacent addresses (figure 4), and the output is in the correct order.

Finally, the 2-step algorithm (also found in Bailey’s paper [PDF]) is a hybrid of the 4 and 6 -step algorithms (figure 5). Rather than inserting transposition steps, columns are copied to temporary vectors before FFTing them and copying them back. Of course, the intermediate transposition and element-wise multiplication can be fused with the copy from temporary vectors.

1.3 Recursively transposing matrices

Transpositions represent a significant portion of the runtime for both 6-step algorithms. This isn’t surprising: good FFTs are memory-bound, and the only steps that aren’t cache-friendly are the three transpositions. Napa-FFT2 generates the initial and final transpositions separately from the middle 4 steps of the 6-step algorithms. This makes it easier to exploit out-of-order input or output.

It also enables us to estimate the time elapsed during each transposition step compared to the rest of the computation (for the range of sizes considered, from 2⁶ to 2²⁵ points). Depending on the size of the input (odd or even powers of two), each transposition (initial or final) adds 5-20% of the runtime of the middle steps. With some algebra we find that, for a full DFT with in-order input and output, the three transposition steps (initial, middle and final) represent 13-40% of the total runtime!

1.3.1 Transposing square matrices

Transposition steps are faster for input sizes that are even powers of two (n = 2^2k). The reason is that the corresponding transposition operates on square matrices of size 2^k× 2^k. These are easily implemented recursively, by decomposing each matrix in four blocks until the base size is reached.

Figure 6: Square in-place transposition

As figure 6 shows, a matrix of size 2^k× 2^k can be transposed in-place by transposing each quadrant in-place, and swapping the top-right and bottom-left quadrants. Napa-FFT2 instead transposes the top-left and bottom-right quadrants in-place, and simultaneously transposes and swaps the two other. The in-place transpositions are simply decomposed recursively. Transpose-and-swap operations are similarly recursively decomposed into four smaller transpose-and-swaps. This recursive decomposition ensures that, for each level of the memory hierarchy (e.g. L1D cache, L2, TLB, L3), some recursion depth is well-suited to that level’s size.

The iterative base case for in-place transposition is not quite a trivial loop nest, so it’s just two nested for loops. Thankfully, it’s only used for blocks directly on the diagonal; it probably doesn’t matter much. Transpose-and-swap is simpler, and represents the vast majority of the computation. The loop nest is manually unrolled-and-jammed to improve spatial locality of the routine, and fully (or nearly) use the data brought in by each cache miss: the outer loop is partially unrolled, and the duplicated inner loops fused (everyone keeps referring to Allen and Cocke’s “A catalogue of optimizing transformations,” but I can’t find any relevant link, sorry). In figure 7, assuming that matrices A and B are in row-major order, accesses to A are naturally in streaming order; the short inner-most loop helps maximise the reuse of (non-consecutive) cache lines in B.

for i below n by 4 
  for j below m 
    for ii from i below i+4 
      operate on A(ii, j), B(j, ii), etc.

1.3.2 Transposing rectangular matrices

Transposing general rectangular matrices is much more difficult than for square, power-of-two–sized, matrices. However, the 6-step algorithms only need to transpose matrices of size 2^k× 2^k+1 or 2^k+1× 2^k. For these shapes, it’s possible to split the input in two square block submatrices, transpose them in-place, and interleave or de-interleave the rows (figure 8).

Figure 8: Rectangular in-place transposition

For now, though, I found it simpler to implement that by transposing the submatrices out-of-place, moving the result to temporary storage (figure 9). The data, implicitly (de-)interleaved, is then copied back.

Figure 9: Rectangular copying transposition

This simplistic implementation explains a lot of the slowdown on odd powers of two sizes. However, even the in-place algorithm would probably be somewhat slower than a square in-place transpose of comparable size: copying rows and tracking whether they have already been swapped into place would still use a lot of cycles.

I believe the block copies could be simplified by going through the MMU. Matrices of 128K complex doubles or more will go through block copies (or swap) of at least 4 KB…the usual page size on x86oids. If the vectors are correctly aligned, we can instead remap pages in the right order. This is far from free, but it may well be faster than actually copying the data. We’re constantly paying for address translation but rarely do anything but mmap address space in; why not try and exploit the hardware better?

1.4 Choosing algorithms

The medium FFT generator produces code for the 2-step algorithm, with smaller FFTs computed by specialised radix-2 code. The copy/FFT/copy loops are manually unroll-and-jammed here too.

The large FFT generator produces code for the 6-step algorithm (without the initial and final transpositions), with smaller FFTs computed either by the radix-2 or 2-step algorithms; the transposition generator is exposed separately. I assume that out-of-order output is acceptable, and only transpose the input, in place. A final transposition would be necessary to obtain in-order output.

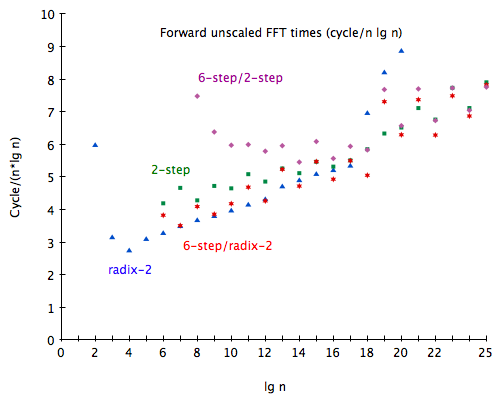
Figure 10 lets us compare the performance of the 4 methods (radix-2, 2-step, 6-step/radix-2 and 6-step/2-step).

Again, radix-2 shows a severe performance degradation as soon as the working set exceeds L3 size. Both 6-step algorithms show spikes in runtimes on odd powers of two: the transposition code isn’t in-place for these vector sizes. On smaller inputs (below ≈ 2¹⁰), 6-step/2-step seems dominated by constant overhead, while the spikes are on even powers of two for 6-step/radix-2. I’m not sure why this is the case for 6-step/radix-2, but the reverse for 2-step.

Table 1 shows the same data, but scaled by the lowest cycle count for each input size; I don’t have confidence intervals, but the spread was extremely low, on the order of 1%.

Radix-2 provides the best performance until n = 2¹², at which point 6-step/radix-2 is better for even powers of two. As input size grows, the gap between radix-2 and 2-step narrows, until n = 2¹⁹, at which point 2-step becomes faster than radix-2. Finally, from n = 2²² onward, 6-step/radix-2 is faster than both radix-2 and 2-step.

On ridiculously large inputs (2²⁵ points or more) 6-step/2-step seems to becomes slightly faster than 6-step/radix-2, reflecting the narrowing gap between radix-2 and 2-step at sizes around 2¹³ and greater. At first sight, it seems interesting to implement 6-step/6-step/radix-2, but this table is for out-of-order results; the 6-step algorithms depend on in-order results from the sub-FFTs, and, for those, 2-step consistently performs better.

2 Napa-FFT2, Bordeaux-FFT, djbfft and FFTW

Choosing the fastest method for each input size, from 2² to 2²⁵, yields the full implementation of Napa-FFT2. The graph in figure 11 illustrates the performance of Bordeaux-FFT, Napa-FFT2 without the final transpose for 6-step, djbfft (which lacks transforms past 2¹³) with out-of-order output, and FFTW (the fastest of in-place and out-of-place for each size, at default planning settings). Napa-FFT2’s, or, rather, radix-2’s, performance curve is pretty much the same as djbfft’s until djbfft’s maximum size is reached. It’s interesting to note that djbfft is written in hand-tuned C, while Napa-FFT2 is machine-generated (SB)CL, without any low-level annotation except type declarations and the elimination of runtime safety checks.

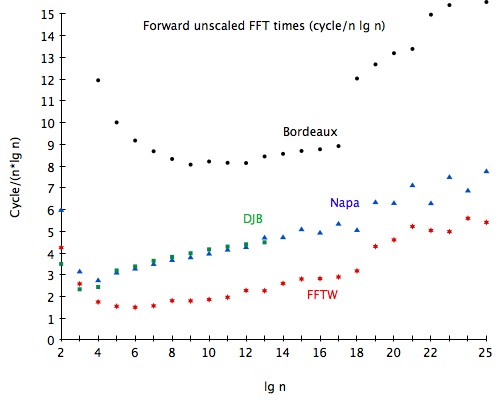
Table 2 presents the same data, scaled by the lowest cycle count. FFTW consistently has the lowest cycle counts. Napa-FFT2 and djbfft are both around twice as slow on small and medium inputs, and, on larger inputs, Napa-FFT2 becomes only 25% to 50% slower than FFTW. Bordeaux-FFT, however, is always around 3 times (or more) as slow as FFTW, and more than 50% slower than Napa-FFT2.

3 What’s next?

The prototype is already pretty good, and definitely warrants more hacking. There are a few obvious things on my list:

• Most of the improvements in the radix-2 generator (larger base cases and making the temporary vector useless) can be ported to Bordeaux-FFT;
• Both the small FFT generator and Bordeaux-FFT could benefit from a split-radix (radix-2/4 instead radix-2) rewrite;
• Scaling (during copy or transpose) is already coded, it must simply be enabled;
• Inverse transforms would be useful;
• In-place rectangular transpositions would probably help reduce the performance gap between odd and even powers of two for the 6-step algorithms;
• Processing real input specially can lead to hugely faster code with little work;
• Generalizing the transposition code to handle arbitrary (power-of-two–sized) matrices would enable easy multidimensional FFTs;
• Finally, I must write a library instead of writing base cases, constant-folding address computations or unrolling (and jamming) loops by hand. It would pretty much be a compiler geared toward large recursively-generated, but repetitive and simple, array-manipulation code.

It’s pretty clear that SBCL’s native support on x86-64 for SSE2 complex float arithmetic pays off. I expect other tasks would similarly benefit from hand-written assembly routines for a few domain-specific operations. SBCL’s architecture makes that very easy. It’s when we want to rewrite patterns across function calls that Python gets in the way…and that’s exactly what code generators should be concerned with getting right.

In the end, I think the most interesting result is that the runtime performance of (SB)CL can definitely be competitive with C for memory-bound tasks like FFT. Common Lisp compilers generally suffer from simplistic, 70’s-style, low-level code generation facilities; luckily, when tackling memory-bound tasks, getting the algorithms and data layouts right to reduce the operation count and exploit hierarchical memory matters a lot more. The advantage of CL is that, unlike C, it’s easy to generate and compile, even at runtime. CL is also easier to debug, since we can enable or disable runtime checks with a single declaration.

If the trend of memory bandwidth (and latency) improving much more slowly than computing power persists, while we keep processing larger data sets, the suitability of Common Lisp to the generation of high-performance code is an asset that will prove itself more and more useful in the near future.

I’m also pleasantly surprised by the performance of Napa-FFT2, regardless of the target language. I’ll probably try and re-implement it in runtime-specialised C (VLBDB, another side-project of mine). This would hopefully help close the gap with FFTW even further, and make it easier to try and exploit MMU tricks.

I’ve been reading some code, and going through some old notes today and I think the following two tricks are too neat not to share.

1 Ticket “spinaphores”

I stumbled upon those in the ia64 section of Linux (arch/ia64/mm/tlb.c); they adjust ticket spinlocks to allow multiple processes in the critical section.

1.1 Ticket spinlocks

LWN has a very good description of Linux’s implementation of ticket spinlocks at http://lwn.net/Articles/267968/.

The basic idea is to have two counters, a ticket counter, and a “now serving” (serve) counter. Both are initialised to 0, and monotonically incremented (with wraparound). Each process that wants to hold the spinlock goes through three steps: acquiring a ticket, waiting for its turn, and releasing the spinlock.

Acquiring a ticket is a fetch-and-add (atomically increment the ticket counter, and return the previous value).

Once a process has a ticket number, it spins on the serve counter until its value is equal to the process’s ticket; the process then holds the spinlock.

Finally, to release the spinlock, a process increments the serve counter, signaling to the next process in line that it’s now its turn.

x86oids have a fairly strong memory model, and Linux exploits that to simplify its ticket locks: both counters are packed in a single word, so that acquiring a ticket and reading the serve counter is a single instruction, and the serve counter is incremented with a half-word instruction (cache coherence and the barrier in fetch-and-add are enough to avoid reordering).

1.2 From locks to counting semaphores

“spinaphores” generalize the serve counter. Instead of serving only the one process whose ticket is equal to the serve counter, they instead serve all the processes whose tickets are inferior to the serve counter. To allow k processes to hold a spinaphore concurrently, the serve counter is simply initialised to k: the serve counter is only incremented when a process releases the spinaphore, so all but the last k processes with low enough tickets have already released the spinaphore. The only other difference with ticket spinlocks is that incrementing the serve counter must also be atomic.

There are some wraparound issues with the definition of “inferior”, but the distance between the ticket and serve counters is bounded by the number of concurrent waiters, which can’t be too large. One can thus define “inferior” as being in [serve-M,serve] (with wraparound), where M is an arbitrary large value (e.g. 2³¹). On a computer, that’s pretty much equivalent to subtracting the ticket and the serve counter and looking at the sign bit.

2 Robin hood hashing

I have been looking for a hash table scheme that work well with modern hardware for a couple years now; Numerical experiments in hashing and There’s more to locality than caches are related to this effort. It seems that most of the good worst-case bounds come from choosing between multiple buckets during insertion (e.g. d-left and cuckoo hashing).

In his Phd thesis “Robin Hood Hashing”, Pedro Celis describes a simple variant of open addressing hashing that also achieves very good worst-case bounds. In fact, in “On worst-case Robin Hood hashing”, Devroye, Morin & Viola find that, for load factors inferior to 1, the worst-case performance of Robin Hood hash tables is pretty much identical to that of multiple-choice hashing schemes ((lg log n), with high probability).

When inserting in regular open addressing tables, the first entry to probe a given cell is allocated to it; the allocation is first-come, first-served. Robin Hood hashing instead bump entries to make sure that lookups don’t have to probe too long: if a new entry hashes to an occupied cell n probes after its initial hash location, while the occupant is only m < n probes away from its own initial location, the current occupant is bumped out and iteratively re-inserted in the table. Intuitively, this policy isn’t useful to improve the average probe length (in fact, it may even worsen it), but rather to reduce the variance of probe lengths, and thus the worst case.

The theoretical results assume independent random probing sequences for each key. In his simulations and numerical experiments, Celis approximated that ideal with double hashing, and found that this small tweak to the usual collision handling scheme results in an exponential improvement in the worst case performance of open addressing hash tables! In fact, some simulations on my end make me believe that the performance might be almost as excellent with linear probing instead of double hashing, which is extremely interesting for cache-friendly hash tables (:

After some theoretical experiments on hash tables, I implemented a prototype for 2-left hash tables with large buckets (16 entries) to see how it’d work in the real world. It worked pretty well, but the way its performance scaled with table size sometimes baffled me. Playing with the layout (despite not fully understanding the initial prototype’s behaviour) helped, but the results were still confounding. The obvious solution was to run microbenchmarks and update my mental performance model for accesses to memory!

(The full set of results are at the end, but I’ll copy the relevant bits inline.)

1 The microbenchmark

The microbenchmark consists of ten million independent repetitions of a small loop that executes an access pattern on 16 independent cache lines. The addresses are generated with a Galois LFSR to minimise the number of uninteresting memory accesses while foiling any prefetch logic.

There are four access patterns. The first pattern, “0”, reads the first word in the line; “0-3” reads the first and fourth words; “0-3-7” reads the first, fourth and eighth (last) words; finally, “0-3-7-8” reads the first, fourth and eighth words of the cache line and the first of the next cache line. It would be interesting to test “0-8”, but it’s not that relevant to my application.

The working sets are allocated in regular pages (4K bytes) or in huge pages (2M bytes) to investigate the effect of the TLB (Translation Lookaside Buffer) when appropriate. A wide number of working set sizes are tested, from 16 KB to 1 GB.

Finally, “Cache miss” measures the number of cache misses (that is, accesses that hit main memory) across the execution of the program, in millions (including a small amount of noise, e.g. to record timings); “TLB miss” measures the number of TLB misses (the TLB caches mappings from logical to physical address), again in millions; and “Cycle/pattern” is the median number of cycles required to execute the access pattern once, computed as the average of 16 independent pattern executions (without compensating for timing or looping overhead, which should be on the order of 20-30 cycles for all 16 executions).

2 Mistake number one: Use the whole cache line, it’s free

CPUs deal with memory one cache line at a time. Barring non-temporal accesses, reading even a single byte results in reading the whole corresponding cache line (64 bytes on current x86oids). Thus, the theory goes, we’re always going to pay for loading the whole cache line from memory and it shouldn’t be any slower to read it all than to access only a single word.

My initial prototype had buckets (of 16 entries) split in two vectors, one for the hash values (four byte each, so one cache line per bucket of hash values), and another for the key-value pairs (more than a cache line per bucket, but the odds of two different keys hashing identically are low enough that it shouldn’t be an issue). Having the hashes in a vector of their own should have improved locality and definitely simplified the use of SSE to compare four hash values at a time.

The in-cache performance was as expected. Reads had a pretty much constant overhead, with some of it hidden by out of order and superscalar execution.

In my microbenchmark, that’s represented by the test cases with working set size from 16KB to 256KB (which all fit in L1 or L2 caches). All the misses are noise (5 million misses for 160 million pattern execution is negligible), and we observe a slow increase for “Cycle/pattern” as the size of the working set and the number of accesses go up.

                +--------------------------------+ 
                |           4K pages             | 
                |    0      0-3    0-3-7  0-3-7-8| 
                +--------------------------------+ 
  Size 16KB     |                                | 
Cache miss (M)  |   3.89    3.85    3.88    3.88 | 
TLB miss   (M)  |   0.50    0.51    0.50    0.58 | 
Cycle/pattern   |   4.50    6.25    6.50    6.50 | 
                |                                | 
                +--------------------------------+ 
  Size 32KB     |                                | 
Cache miss (M)  |   3.79    3.87    3.86    3.88 | 
TLB miss   (M)  |   0.52    0.51    0.50    0.50 | 
Cycle/pattern   |   4.75    6.25    6.25    6.50 | 
                |                                | 
                +--------------------------------+ 
  Size 128KB    |                                | 
Cache miss (M)  |   3.80    3.67    3.84    3.66 | 
TLB miss   (M)  |   0.52    0.36    0.50    0.39 | 
Cycle/pattern   |   5.25    6.25    6.50    7.25 | 
                |                                | 
                +--------------------------------+ 
  Size 256KB    |                                | 
Cache miss (M)  |   5.03    5.07    5.07    4.06 | 
TLB miss   (M)  |   0.51    0.50    0.51    0.47 | 
Cycle/pattern   |   5.25    6.50    7.25    7.25 | 
                |                                | 
                +--------------------------------+

Once we leave cache, for instance at 128MB, things get weirder:

                +--------------------------------+ 
                |           4K pages             | 
                |    0     0-3    0-3-7  0-3-7-8 | 
                +--------------------------------+ 
  Size 128MB    |                                | 
Cache miss (M)  | 153.21  153.35  296.01  299.06 | 
TLB miss   (M)  | 158.00  158.07  158.10  160.58 | 
Cycle/pattern   |  30.50   34.50   41.00   44.00 | 
                |                                | 
                +--------------------------------+

According to my theory, the cost for accessing additional words in the same cache line should be negligible compared to loading it from memory. Yet, “Cycle/pattern” increases slowly but regularly. I believe that the reason for that is that memory controllers don’t read a full cache line at a time. When an uncached address is accessed, the CPU does load the whole line into cache, but only in multiple steps.

The first step also executes much slower than the others because of the way memory is addressed in RAM: addresses are sent in two halves, first the “column”, and then the “row”. To read an arbitrary address, both halves must be sent, one after the other. Reading an address close to the previous one, however, only updates the row.

It’s also interesting to note that both patterns “0-3-7” and “0-3-7-8” trigger about twice as many cache misses as “0” and “0-3”. Yet, “0-3-7” only reads from one cache line, while “0-3-7-8” reads from two. I believe that’s because of prefetching. We’ll come back to the issue of multiple reads from out-of-cache memory later.

So, while it is true that it’s better to fully use a cache line (because it’ll be completely read regardless), reading more words still incurs additional latency, and it’s only slightly cheaper than hitting an adjacent cache line.

3 Mistake number two: Cache misses dominate everything else

In response to my better understanding of memory, I changed the layouts of my buckets to minimise the expected number of reads. In the end, I decided to pack each bucket’s hash values in a header of 128 bit (the size of an XMM register). With 16 bytes used for the hash values, I could append 15 key-value pairs to have a round size of 256 bytes per bucket, and execute only adjacent accesses on successful lookups. The extra 16^th hash value stored the number of entries in the bucket.

So, instead of having one vector of hash buckets and one of value buckets per subtable (and two subtables per hash table):

struct entry { 
        u64 key, val; 
}; 
 
struct hash_bucket { 
        u32 hashes[16]; 
}; 
 
struct value_bucket { 
        struct entry entries[16]; 
};

I had:

struct bucket { 
        union { 
                vu8 pack; // SSE vector of u8 
                u8  vec[16]; 
        } hash; 
        struct entry entries[15]; 
};

The new layout meant that I only had one byte of hash value for each entry. It wasn’t such an issue, since I was already computing two independent hash values per key (for the two subtables). When working with the right subtable, I could simply store the hash value from the left subtable (but still index buckets with the right subtable’s hash value), and vice versa. Since the hashes are independent, the odds of false positives are on the order of 5%. According to my new-found knowledge, this should perform really well: only one access to scan the hash values, and then, when the hash values match, the key-value pairs are at adjacent addresses.

The histogram of timings for inserts and lookups did improve and even showed nice, steep peaks (depending on whether one or two subtables were probed). Yet, there was still something really hard to explain: I seemed to run out cache much earlier than expected.

I have 256KB of L2 cache, and 12MB of L3 on my machine... but, in my microbenchmark, we observe drastic changes in timings even between working sets of 2MB and 8MB:

                +--------------------------------+ 
                |           4K pages             | 
                |    0     0-3    0-3-7  0-3-7-8 | 
                +--------------------------------+ 
  Size 2MB      |                                | 
Cache miss (M)  |   5.06    5.10    5.11    5.14 | 
TLB miss   (M)  |   0.67    0.85    0.88    0.90 | 
Cycle/pattern   |   6.50    7.25    8.75   10.75 | 
                |                                | 
                +--------------------------------+ 
  Size 8MB      |                                | 
Cache miss (M)  |   7.29    7.28    8.67    8.68 | 
TLB miss   (M)  | 120.45  120.55  120.63  122.52 | 
Cycle/pattern   |  11.00   13.00   15.50   17.25 | 
                |                                | 
                +--------------------------------+

The access times nearly double, for working sets that both are much larger than L2 but do fit in L3 (as evidenced by the very low number of cache misses). This is where the “TLB miss” row is interesting: the number of TLB misses goes from negligible to nearly one miss per access (each access to memory triggers a TLB lookup to map from logical to physical address). The L2 TLB on my machine holds 512 pages, at 4K each, for a total of 2MB; a working set not fitting in TLB has as much of an impact as not fitting in cache!

I should have thought of that: people who ought to know like kernel developers or Kazushige Goto (of GotoBLAS and libflame fame) have been writing about the effect of TLB misses since at least 2005. So, I used huge pages (2MB instead of 4KB) and observed a return to sanity. On my microbenchmark, this shows up as:

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 2MB      |                                :                                 | 
Cache miss (M)  |   5.06    5.10    5.11    5.14 :   5.03   5.01    5.02    5.05   | 
TLB miss   (M)  |   0.67    0.85    0.88    0.90 :   0.23   0.27    0.23    0.24   | 
Cycle/pattern   |   6.50    7.25    8.75   10.75 :   5.25   6.75    7.75    9.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 8MB      |                                :                                 | 
Cache miss (M)  |   7.29    7.28    8.67    8.68 :   5.21   5.22    5.22    5.25   | 
TLB miss   (M)  | 120.45  120.55  120.63  122.52 :   0.23   0.30    0.27    0.25   | 
Cycle/pattern   |  11.00   13.00   15.50   17.25 :   5.00   6.75    7.75   10.00   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

Using huge pages cuts the times by almost 50% on the microbenchmark; that’s on par the difference between L3 and L1 (only ≈ 33%, but timing overhead is much more significative for L1). More importantly, the timings are the same for two working sets that fit in L3 but largely spill out of L2.

Improvements are almost as good when hitting main memory:

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 16MB     |                                :                                 | 
Cache miss (M)  |  49.37   49.41   90.72   91.77 :  47.82  47.72   81.46   88.01   | 
TLB miss   (M)  | 140.59  140.60  140.67  142.87 :   0.25   0.25    0.24    0.25   | 
Cycle/pattern   |  18.00   20.50   24.00   26.50 :  14.00  15.25   17.00   18.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 32MB     |                                :                                 | 
Cache miss (M)  | 106.93  107.09  203.73  207.82 : 106.55  106.62  186.50  206.83  | 
TLB miss   (M)  | 150.56  150.74  150.82  153.09 :   0.24   0.26    0.25    0.27   | 
Cycle/pattern   |  22.25   24.75   31.00   34.00 :  15.75  17.25   20.00   27.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 64MB     |                                :                                 | 
Cache miss (M)  | 137.03  137.23  263.73  267.88 : 136.67  136.82  232.64  266.93  | 
TLB miss   (M)  | 155.63  155.79  155.81  158.21 :   5.09   5.25    5.69    5.78   | 
Cycle/pattern   |  26.00   29.25   36.75   39.75 :  16.75  18.25   24.25   30.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

The access times are much better (on the order of 30% fewer cycles), but they also make a lot more sense: the difference in execution time between working sets that don’t fit in last level cache (L3) is a lot smaller with huge pages. Moreover, now that TLB misses are out of the picture, accesses to two cache lines (“0-3-7-8”) are almost exactly twice as expensive as an access to one cache line (“0”).

My test machine has a 32 entry TLB for 2M pages (and another 32 for 4M pages, but my kernel doesn’t seem to support multiple huge page sizes). That’s enough for 64 MB of address space. Indeed, we observe TLB misses with larger working sets:

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 128MB    |                                :                                 | 
Cache miss (M)  | 153.21  153.35  296.01  299.06 : 152.77  152.86  261.09  298.71  | 
TLB miss   (M)  | 158.00  158.07  158.10  160.58 :  80.84   84.96   91.48   96.40  | 
Cycle/pattern   |  30.50   34.50   41.00   44.00 :  18.75   20.75   27.25   33.25  | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 512MB    |                                :                                 | 
Cache miss (M)  | 170.65  170.90  326.84  329.59 : 169.90  170.22  286.47  326.54  | 
TLB miss   (M)  | 160.39  160.41  162.17  164.62 : 140.35  147.28  160.81  179.58  | 
Cycles/patterm  |  36.75   41.00   47.00   50.00 :  20.50  23.00   29.75   35.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 1GB      |                                :                                 | 
Cache miss (M)  | 184.29  184.29  353.23  356.73 : 180.11  180.43  300.66  338.62  | 
TLB miss   (M)  | 163.64  164.26  176.04  178.88 : 150.37  157.85  169.58  190.89  | 
Cycle/pattern   |  37.25   41.50   52.00   55.25 :  22.00  24.75   30.50   37.00   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

However, even with a working set of 1GB, with nearly as many TLB misses for huge as for regular pages, we see a reduction in timing by 30-40%. I think that’s simply because the page table fits better in cache and is quicker to search. 1GB of address space uses 256K pages (at 4KB each). If each page descriptor uses only 16 bytes (one quad word for the logical address and another for the physical address), that’s still 4MB for the page table!

4 TL;DR

• Multiple accesses to the same cache line still incur a latency overhead over only one access (but not in memory throughput, since the cache line will be fully read anyway).
• Use huge pages if you can. Otherwise, you’ll run out of TLB space at about the same time as you’ll leave L2 (or even earlier)... and TLB misses are more expensive than L2 misses, almost as bad as hitting main memory.
• Prefer accessing contiguous cache lines. If you can’t use huge pages or if your working set is very large, only one TLB miss is incurred for accesses to lines in the same page. You might also benefit from automatic prefetching.
• This is why cache-oblivious algorithms are so interesting: they manage to take advantage of all those levels of caching (L1, L2, TLB, L3) without any explicit tuning, or even considering multiple levels of caches.

The test code can be found at http://discontinuity.info/~pkhuong/cache-test.c.

I could have tried to tweak the layout of my 2-left hash table some more in reaction to my new cost model. However, it seems that it’s simply faster to hit multiple contiguous cache lines (e.g. like linear or quadratic probing) than to access a few uncorrelated cache lines (2-left or cuckoo hashing). I’m not done playing with tuning hash tables for caches, though! I’m currently testing a new idea that seems to have both awesome utilisation and very cheap lookups, but somewhat heavier inserts. More on that soon(ish).

5 Annex: full tables of results from the microbenchmark

• Test machine: unloaded 2.8 GHz Xeon (X5660) with DDR3-1333 (I don’t remember the timings)
• Cache sizes:
  • L1D: 32 KB
  • L2: 256 KB
  • L3: 12 MB
• TLB sizes
  • L1 dTLB (4KB): 64 entries
  • L1 dTLB (2M):32 entries
  • L2 TLB (4 KB): 512 entries

Benchmark description: access 16 independent cache lines, following one of four access patterns. 10M repetitions (with different addresses). Test with regular 4KB pages and with huge pages (2MB). Report the total number of cache and TLB misses (in million), and the median of the number of cycle per repetition (divided by 16, without adjusting for looping or timing overhead, which should be around 30 cycles per repetition). Source at http://discontinuity.info/~pkhuong/cache-test.c.

Access patterns:

• 0: Read the cache line’s first word
• 0-3: Read the cache line’s first and fourth words
• 0-3-7: Read the cache line’s first, fourth and eighth words
• 0-3-7-8: Read the cache line’s first, fourth and eighth words, and the next cache line’s first word

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 16KB     |                                :                                 | 
Cache miss (M)  |   3.89    3.85    3.88    3.88 :   3.58   3.78    3.78    3.79   | 
TLB miss   (M)  |   0.50    0.51    0.50    0.58 :   0.16   0.25    0.25    0.25   | 
Cycle/pattern   |   4.50    6.25    6.50    6.50 :   4.50   6.25    6.50    6.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 32KB     |                                :                                 | 
Cache miss (M)  |   3.79    3.87    3.86    3.88 :   3.77   3.78    3.78    3.78   | 
TLB miss   (M)  |   0.52    0.51    0.50    0.50 :   0.25   0.24    0.26    0.24   | 
Cycle/pattern   |   4.75    6.25    6.25    6.50 :   4.75   6.25    6.25    6.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 128KB    |                                :                                 | 
Cache miss (M)  |   3.80    3.67    3.84    3.66 :   3.76   3.77    3.77    3.78   | 
TLB miss   (M)  |   0.52    0.36    0.50    0.39 :   0.26   0.26    0.24    0.26   | 
Cycle/pattern   |   5.25    6.25    6.50    7.25 :   5.25   6.25    6.50    7.25   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 256KB    |                                :                                 | 
Cache miss (M)  |   5.03    5.07    5.07    4.06 :   3.98   3.98    3.83    3.83   | 
TLB miss   (M)  |   0.51    0.50    0.51    0.47 :   0.27   0.26    0.23    0.25   | 
Cycle/pattern   |   5.25    6.50    7.25    7.25 :   5.25   6.25    6.75    7.25   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 1MB      |                                :                                 | 
Cache miss (M)  |   5.04    5.09    5.09    5.09 :   5.00   4.99    5.00    4.99   | 
TLB miss   (M)  |   0.50    0.50    0.49    0.50 :   0.23   0.25    0.24    0.24   | 
Cycle/pattern   |   6.25    7.25    8.50   10.50 :   5.25   6.75    7.75    9.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 2MB      |                                :                                 | 
Cache miss (M)  |   5.06    5.10    5.11    5.14 :   5.03   5.01    5.02    5.05   | 
TLB miss   (M)  |   0.67    0.85    0.88    0.90 :   0.23   0.27    0.23    0.24   | 
Cycle/pattern   |   6.50    7.25    8.75   10.75 :   5.25   6.75    7.75    9.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 4MB      |                                :                                 | 
Cache miss (M)  |   5.19    5.19    5.19    5.22 :   5.08   5.07    5.08    5.11   | 
TLB miss   (M)  |  80.42   80.59   80.70   81.98 :   0.24   0.25    0.24    0.24   | 
Cycle/pattern   |   8.25   10.00   12.00   13.75 :   5.00   6.75    7.75    9.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 8MB      |                                :                                 | 
Cache miss (M)  |   7.29    7.28    8.67    8.68 :   5.21   5.22    5.22    5.25   | 
TLB miss   (M)  | 120.45  120.55  120.63  122.52 :   0.23   0.30    0.27    0.25   | 
Cycle/pattern   |  11.00   13.00   15.50   17.25 :   5.00   6.75    7.75   10.00   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 16MB     |                                :                                 | 
Cache miss (M)  |  49.37   49.41   90.72   91.77 :  47.82  47.72   81.46   88.01   | 
TLB miss   (M)  | 140.59  140.60  140.67  142.87 :   0.25   0.25    0.24    0.25   | 
Cycle/pattern   |  18.00   20.50   24.00   26.50 :  14.00  15.25   17.00   18.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 32MB     |                                :                                 | 
Cache miss (M)  | 106.93  107.09  203.73  207.82 : 106.55  106.62  186.50  206.83  | 
TLB miss   (M)  | 150.56  150.74  150.82  153.09 :   0.24   0.26    0.25    0.27   | 
Cycle/pattern   |  22.25   24.75   31.00   34.00 :  15.75  17.25   20.00   27.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 64MB     |                                :                                 | 
Cache miss (M)  | 137.03  137.23  263.73  267.88 : 136.67  136.82  232.64  266.93  | 
TLB miss   (M)  | 155.63  155.79  155.81  158.21 :   5.09   5.25    5.69    5.78   | 
Cycle/pattern   |  26.00   29.25   36.75   39.75 :  16.75  18.25   24.25   30.75   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

                +--------------------------------+---------------------------------+ 
                |           4K pages             :          2M pages               | 
                |    0     0-3    0-3-7  0-3-7-8 :   0      0-3    0-3-7   0-3-7-8 | 
                +--------------------------------+---------------------------------+ 
  Size 128MB    |                                :                                 | 
Cache miss (M)  | 153.21  153.35  296.01  299.06 : 152.77  152.86  261.09  298.71  | 
TLB miss   (M)  | 158.00  158.07  158.10  160.58 :  80.84   84.96   91.48   96.40  | 
Cycle/pattern   |  30.50   34.50   41.00   44.00 :  18.75   20.75   27.25   33.25  | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 512MB    |                                :                                 | 
Cache miss (M)  | 170.65  170.90  326.84  329.59 : 169.90  170.22  286.47  326.54  | 
TLB miss   (M)  | 160.39  160.41  162.17  164.62 : 140.35  147.28  160.81  179.58  | 
Cycles/patterm  |  36.75   41.00   47.00   50.00 :  20.50  23.00   29.75   35.50   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+ 
  Size 1GB      |                                :                                 | 
Cache miss (M)  | 184.29  184.29  353.23  356.73 : 180.11  180.43  300.66  338.62  | 
TLB miss   (M)  | 163.64  164.26  176.04  178.88 : 150.37  157.85  169.58  190.89  | 
Cycle/pattern   |  37.25   41.50   52.00   55.25 :  22.00  24.75   30.50   37.00   | 
                |                                :                                 | 
                +--------------------------------+---------------------------------+

N.B. A pdf version is also available.

My girlfriend gave me Warren’s Hacker’s Delight for Christmas. It’s really a nice compendium of tricks that are usually available on the web, but strewn across a dozen websites.

I only started reading it this morning, and I figured I’d put some of my notes here instead of leaving them in the margins. The page numbers refer to the ninth printing.

1 2-5: Sign Extension (p. 18)

For sign extension (i.e. replicate the k^th bit to the left), Warren suggests (for sign extension of a byte into a word):

1. ((x + 0x00000080) & 0x000000FF) -0x00000080
2. ((x & 0x000000FF) ⊕0x00000080) -0x00000080

When one knows that the higher bits of x are all zero, the second variant becomes (x ⊕0x00000080) -0x00000080. A similar variant is x|- (x & 0x00000080).

Warren’s variant doesn’t require any temporary register, but needs a single constant twice. Mine only requires that constant once, but needs a temporary register. On x86, with its good support for constant operands, Warren’s is probably preferable. With a RISCier ISA, the other version could be useful.

2 2-9: Decoding a “Zero Means 2**n” Field (p. 20)

The idea here is that we have a field which will never take a value of 0; it could however, take any value from 1 to 2ⁿ. We obviously want to pack this into exactly n bits. A simple encoding would simply map 0 to 1, 1 to 2, etc. For various reasons, we’re sometimes stuck with an encoding where everything except 0 maps to itself, and 0 to 2ⁿ.

Notice that 0 ≡ 2ⁿ mod 2ⁿ. What we want to do is perform an identity modulo 2ⁿ, but skip the modulo on the final result. Obvious candidates are x - 1 + 1, x + 1 - 1 and 0 --x (and since we’re working modulo 2ⁿ, -1 ≡ 2ⁿ- 1 and 0 ≡ 2ⁿ).

From Warren’s list of eight “identities” (for 2ⁿ = 8), three clearly fall from the above:

1. ((x - 1) & 7) + 1
2. 8 - (-x & 7)
3. ((x + 7) & 7) + 1

Interestingly, those involving  |  - 8 also do! x |  - 8 computes (x & 7) - 8: it’s sending x to a representative from its equivalence class modulo 8, but to the smallest negative value, instead of the smallest positive value. The intuition is that, like masking with 7, all but the three low bits are discarded; however, instead of filling the rest with 0s, like & 7, |  - 8 fills them with 1s.

3 Extra! Extra!

This entry is more markup-heavy than usual. That would be because I’m actually typing this in LATEX, while a Lisp script drives the conversion (via tex4ht) into XHTML for pyblosxom. You can find the script at http://discontinuity.info/\~pkhuong/tex2blosxom.lisp. It’s a hack, but it works!

In February this year, Nathan Froyd described allocation sequences in SBCL and alternative approaches other implementations use to make sure the runtime never sees half-initialised objects. At first sight, SBCL's sequence seems fairly large and slow for what, in the end, increments a thread-local pointer, even on x86-64, with its awesome 14 (RBP actually serves as a frame pointer in SBCL) GPRs:

    Set the pseudo-atomic bit
OR BYTE PTR [R12+160], 8

    (what you'd expect for bump:) Load the allocation pointer
MOV R11, [R12+80]
    Test for overflow
LEA RDX, [R11+16]
CMP [R12+88], RDX
    Jump to an out of line sequence
JBE L4
    Or save incremented pointer
MOV [R12+80], RDX
    ... and tag it
LEA RDX, [R11+7]
    (end of allocation per se)

    Finally, unset the pseudo-atomic bit
XOR BYTE PTR [R12+160], 8
    Check for interrupt pending
JEQ L2
    Trigger a signal if so
BREAK 9                    ;      pending interrupt trap
L2: ...

That's two load/store and a test just to make sure we're not caught with our pants down, handling improperly initialised objects.

One element of the alternatives is to actively check for pending interrupts (or GCs, etc). Instead of allowing interruptions everywhere except around key sequences, interruptions are queued, and explicit checks inserted by the compiler. That seems like an interesting implementation choice, so I wanted to see what it'd look like in SBCL.

It was pretty easy to adapt the compiler to insert such checks at appropriate locations (in the current case, at the end of each function' prologue, and at the head of loops). Using memory protection to turn an access into a conditional interruption seemed like a good idea, and that's what I quickly implemented.

These checks can be executed fairly often in tight loops, so it's important that they be very efficient. The first version loaded a magic address from thread-local storage (an address pointed to by a register), and then wrote to that address. When the thread had to be interrupted, the page containing that address was made unreadable and unwritable, so the last access triggered a segfault, which was then handled specially.

The result was slow... 25% as much time as the original (signals-ful) version for a simple (loop repeat n do [not cons]) function, and no difference for a consing loop. Modifying the safepoint sequence to read from the magic address instead of writing to it halved the slowdown to ~10%, and did not improve the runtime of the consing loop. That's still far from impressive.

Executing two instructions at each safepoint seems obviously fishy. Indeed, things improved sensibly when the safepoint sequence became a single TEST, as in Nathan's example from HotSpot. Instead of having to read an arbitrary address from the thread struct, I moved the "magic page" to a fixed offset from the thread structure. The safepoint sequence then became a single instruction, TEST EAX, [THREAD_STRUCT_REG + offset] (a register is dedicated to thread-local storage). That's a single instruction, reads from memory and does not clobber any register. Unfortunately, that was only enough to bring the runtime for safepoints to the same level (+/- 1-2%) as that of the original code (it does save ~50 KB out of 40 MB on the x86-64 core :).

I'm not sure how to explain the results, except by saying that x86-64 (both Core 2 and K10) memory subsystems are awesome. In any case, unless I was doing something extremely wrong, the current XOR/XOR/JEQ/BREAK sequence seems to perform well, even when compared to what other implementations (not constrained by any systems programming goal) do. There still are reasons to look into a safe point system for SBCL (simpler to reason about, easier to avoid certain states, easier to manipulate where and when interruptions can happen, ...), but performance doesn't seem to be one of them.

SWAR (SIMD Within A Register) codes can portably express short-vector parallelism for operations on small packed data (e.g. byte or even nybble vectors). A trivial application of the technique is when we test whether any bit in a word is set (equal to 1) by comparing the whole word against 0. Obviously, that also work to test whether any field (of arbitrary width) is not filled with 0. This document, from 1997, provides a fairly clear and complete overview.

Just like testing whether any bit is set, it is easy to find whether some bit is not set (it's simply the opposite of whether every bit in the word is set). Things are more complex when the data are wider than a single bit (but obviously narrower than a full word). I found a short implementation (and barely tested it), but it might be possible to do even shorter. Skip to the series of asterisks if you want to solve that puzzle (to efficiently find whether any field in a sequence of data, itself packed into a single word, is 0) yourself.

To simplify the description, I'll assume that we're working with 4-bit-wide fields. It should be clear how the code can be adapted to other widths or even mixed widths.

Let x = aaaabbbbccccdddd... be the input.

1. x' = x | (x >> 1). The first bit in each field is now, for our purposes, noise. However, some of the remaining 3 bits are now non-zero iff some the original 4 were.

2. ones = x' & ~0x8888.... The noise bits are masked out.

3. borrow = 0x8888... - ones. The first bit of each field in borrow is 0 iff some of the 3 other bits in ones aren't (iff some of the 4 bits in x weren't).

4. result = borrow & 0x8888... is zero iff the first bit of every field in borrow is 0 (iff every field in x was non-null).

And, finally, that is easy to test for, a word at a time. In the end, it takes 5 (hopelessly serial) operations (>>, |, &, - and &) and a conditional branch.

**** Testing whether any field in a word is filled with 0 may seem incredibly obscure. Apart from (some #'zerop [packed-unboxed-vector]), what use is there for such code sequences? One trick is to exploit xor. xor lets us compare multiple fields at a time: a field is 0 in a xor b iff the corresponding fields in a and b are identical (bit for bit). Now that we can determine when at least one pair of fields is equal, it's simple to implement, e.g., default FIND on specialised vectors without having to test each datum separately (until the very end, when we know that one of the pairs is equal, but not which). As usual, a full implementation, capable of dealing with :start, :end and displaced vectors is a lot more work.

Integer division (and its kissing cousins, remainder and modulo) is an operation that regularly pops up in surprising places. The first time I encountered the problem was a few years ago, when I wanted to implement a corewar VM in SBCL (probably my first attempt at a real project in CL). My program was much slower than I would have expected: constant MOD were compiled to actual divisions. More recently, I hit the same problem when trying to implement hash functions and PRNGs efficiently. The main technique to make such operation decently fast approximates division by a multiplication and a shift (in other words, multiplication by a fraction). However, there are other tricks in more restricted situations that can sometimes yield simpler code.

Expressing division as a multiplication is actually simple when you think of it in terms of fractions. Division (and then truncation) by x is like multiplication by 1/x. Since the only type of division we can easily express is division by a power of 2, we want to approximate multiplication by 1/x with a multiplication by y/2^k. Moreover, since the result will be truncated, we want to overapproximate (in absolute value) the fraction. We thus find (for x positive) the folklore formula y = ceiling(2^k/x) (or 1 + floor(2^k/x), which suffers from an off-by-one when x is a power of 2). Note that since the multiplier is rounded up, any error will be one of overapproximation. If the sign of the input is known (or the range otherwise asymetric), it is possible to use a small additive constant to bring the result of the multiplication closer to 0 before dividing and taking the floor (with a shift), and reduce the overapproximation.

In http://www.discontinuity.info/~pkhuong/pseudoinverse.pdf, we find a nice way to figure out the smallest z such that floor(z/x) is different from floor(z*y/2^k). If the input is known to fit in the range (which is often on the order of machine ints), then it is possible to convert integer division to multiplication. Unfortunately, this doesn't even consider the possibility of a (constant) additive fixup between multiplication and division/flooring.

When implementing this on a machine that offers BxB -> B, B multiplication (e.g., 32x32 -> 32, 32 on IA32, or 64x64 -> 64, 64 on x86-64), or even just the most significant half (like Itanium or Alpha), there are two main interesting values for k (as in y/2^k): B and B + floor(lg x). If we take k = B, then we can simply use the most significant word as an implicitly shifted value. If that isn't precise enough, then B + floor(lg x) is the largest denominator such that y (skipping leading zeros) will fit in B bits; the result must however then be shifted. In both cases, but especially when shifting, it is essential to ensure that the result won't overflow the space available in the significant half of the product. When a machine offers many multiplication sizes, it can be useful to try smaller ones first: wider multiplications are sometimes slower, and larger constant always take up more space.

Sometimes, we're only interested in the remainder (MOD is slightly more complex and can be expressed in terms of REM). In the general case, it is impossible to avoid a division, or at least a multiplication by a pseudoinverse, followed by a multiplication and a subtraction. However, when the input range is restricted, some nice tricks are available. It's much simpler to assume that the input is always positive (or always negative). Doing otherwise requires a non-trivial amount of mask generation and subsequent masking, making the tricks less attractive.

Apart from powers of 2, the most obvious trick is when we want (rem z x), where z is known to be smaller than 2x. We can express x as 2^n - e. We have (rem z x) = z if z < x, and (rem z x) = z-x otherwise. It would be simple to compare, generate a mask and do a masked subtraction. However, when z + e might overflow (and n is the width of the register), a simple way to check for that is to add e to z. If the result is greater than 2^n - 1, z >= x (but we still have z < 2^(n+1)). Luckily, the implicit wrap around (masking off everything but the lower n bits) is enough to subtract x (remember that e was previously added, so subtracting 2^n really subtracts x). If z < x (the overflow bit isn't set), then we have to subtract e back. This logic can easily be expressed with a masked subtraction.

A slightly more widely applicable trick is also based on representing the modulo x as 2^k - e. We can split z in 2 (or more) parts: z = z1 2^k + z0. Thus (rem z x) = (rem (z1 e + z0) x). If the product z1 e is small enough, we can then use the previous trick instead of computing the remainder the usual way (it would be possible to recurse). By adding e to z1 e and then adding that to z0 we can guarantee that any overflow will only happen in the last addition, thus making it possible to easily use hardware flags.

Official SBCL should be able to express some of these tricks (at the very least reciprocal multiplication) some time soon. The neat thing about optimising divisions away is that they're so expensive (on the order of 100-200 clock cycles on modern x86) that even branches are pretty much guaranteed to be an improvement, even in the worst case :)