Two variations on old themes
I’ve been reading some code, and going through some old notes today and I think the following two tricks are too neat not to share.
1 Ticket “spinaphores”
I stumbled upon those in the ia64 section of Linux (arch/ia64/mm/tlb.c); they
adjust ticket spinlocks to allow multiple processes in the critical section.
1.1 Ticket spinlocks
LWN has a very good description of Linux’s implementation of ticket spinlocks at http://lwn.net/Articles/267968/.
The basic idea is to have two counters, a ticket counter, and a “now serving” (serve) counter. Both are initialised to 0, and monotonically incremented (with wraparound). Each process that wants to hold the spinlock goes through three steps: acquiring a ticket, waiting for its turn, and releasing the spinlock.
Acquiring a ticket is a fetch-and-add (atomically increment the ticket counter, and return the previous value).
Once a process has a ticket number, it spins on the serve counter until its value is equal to the process’s ticket; the process then holds the spinlock.
Finally, to release the spinlock, a process increments the serve counter, signaling to the next process in line that it’s now its turn.
x86oids have a fairly strong memory model, and Linux exploits that to simplify its ticket locks: both counters are packed in a single word, so that acquiring a ticket and reading the serve counter is a single instruction, and the serve counter is incremented with a half-word instruction (cache coherence and the barrier in fetch-and-add are enough to avoid reordering).
1.2 From locks to counting semaphores
“spinaphores” generalize the serve counter. Instead of serving only the one process whose ticket is equal to the serve counter, they instead serve all the processes whose tickets are inferior to the serve counter. To allow k processes to hold a spinaphore concurrently, the serve counter is simply initialised to k: the serve counter is only incremented when a process releases the spinaphore, so all but the last k processes with low enough tickets have already released the spinaphore. The only other difference with ticket spinlocks is that incrementing the serve counter must also be atomic.
There are some wraparound issues with the definition of “inferior”, but the
distance between the ticket and serve counters is bounded by the number of
concurrent waiters, which can’t be too large. One can thus define “inferior” as being
in [serve-M,serve] (with wraparound), where M is an arbitrary large value (e.g.
231). On a computer, that’s pretty much equivalent to subtracting the ticket and the
serve counter and looking at the sign bit.
2 Robin hood hashing
I have been looking for a hash table scheme that work well with modern hardware for a couple years now; Numerical experiments in hashing and There’s more to locality than caches are related to this effort. It seems that most of the good worst-case bounds come from choosing between multiple buckets during insertion (e.g. d-left and cuckoo hashing).
In his Phd thesis “Robin Hood Hashing”, Pedro Celis describes a simple variant
of open addressing hashing that also achieves very good worst-case bounds. In fact,
in “On worst-case Robin Hood hashing”, Devroye, Morin & Viola find that, for load
factors inferior to 1, the worst-case performance of Robin Hood hash tables is pretty
much identical to that of multiple-choice hashing schemes (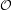 (lg log n), with high
probability).
(lg log n), with high
probability).
When inserting in regular open addressing tables, the first entry to probe a given cell is allocated to it; the allocation is first-come, first-served. Robin Hood hashing instead bump entries to make sure that lookups don’t have to probe too long: if a new entry hashes to an occupied cell n probes after its initial hash location, while the occupant is only m < n probes away from its own initial location, the current occupant is bumped out and iteratively re-inserted in the table. Intuitively, this policy isn’t useful to improve the average probe length (in fact, it may even worsen it), but rather to reduce the variance of probe lengths, and thus the worst case.
The theoretical results assume independent random probing sequences for each key. In his simulations and numerical experiments, Celis approximated that ideal with double hashing, and found that this small tweak to the usual collision handling scheme results in an exponential improvement in the worst case performance of open addressing hash tables! In fact, some simulations on my end make me believe that the performance might be almost as excellent with linear probing instead of double hashing, which is extremely interesting for cache-friendly hash tables (:
