I’ve been thinking about stream processing again, and came back to an old pick-two-of-three conjecture of mine: for stream processing without dynamic allocation, “arbitrary outputs per input, multiple consumers, multiple producers: choose two.”
The question is interesting because stream processing in constant space is a subset of L (or FL, and thus probably not P-complete, let alone Turing complete. Having easily characterisable subsets of stream processing that can be implemented in constant space would be a boon for the usability of stream DSLs.
I think I find this academic trope as suspicious as @DRMavIver does, so I have mixed feelings about the fact that this one still feels true seven years later.
Is it just me or do impossibility theorems which claim "these three obviously desirable properties cannot simultaneously be satisfied" always include at least one obviously undesirable or at least suspicious property?
— David R. MacIver (@DRMacIver) June 19, 2018
The main reason I believe in this conjecture is the following
example, F(S(X), X), where S is the function that takes a stream
and ouputs every other value. Or, more formally, \(F\sb{i} = f(X\sb{2i}, X\sb{i})\).
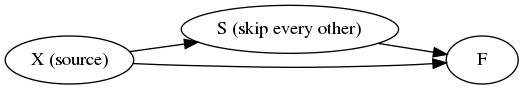
Let’s say X is some stream of values that can’t be easily
re-computed (e.g., each output value is the result of a slow
computation). How do we then compute F(S(X), X) without either
recomputing the stream X, or buffering an unbounded amount of past
values from that stream? I don’t see a way to do so, not just in any
stream processing DSL (domain specific language), but also in any
general purpose language.
For me, the essence of the problem is that the two inputs to F are
out of sync with respect to the same source of values, X: one
consumes two values of X per invocation of F, and the other only
one. This issue could also occur if we forced stream transducers
(processing nodes) to output a fixed number of value at each
invocation: let S repeat each value of X twice,
i.e., interleave X with X (\(F\sb{i} = f(X\sb{\lfloor i / 2\rfloor}, X\sb{i})\)).
Forcing each invocation of a transducer to always produce exactly one value is one way to rule out this class of stream processing network. Two other common options are to forbid either forks (everything is single-use or subtrees copied and recomputed for each reuse) or joins (only single-input stream processing nodes).
I don’t think this turtle-and-hare desynchronisation problem is a weakness in stream DSLs, I only see a reasonable task that can’t be performed in constant space. Given the existence of such tasks, I’d like to see stream processing DSLs be explicit about the tradeoffs they make to balance performance guarantees, expressiveness, and usability, especially when it comes to the performance model.