This post was written under the influence of coffee ice cream and espresso. It’s a magical drink ;)

I don’t really follow the compression scene, and only pay minimal attention to machine learning. Nevertheless, the “Compression is Learning” slogan feels more and more right to me. In this post, I’ll explore another relationship that I find surprising: one between compression and compilation.

Five years ago, I took Marc Feeley’s compiler class, and he let us choose our term project. I settled on generating traces from recursive algorithms (typical of cache-oblivious algorithms) and reordering them to get iterative code that was better suited to the first level of cache. I came up with a gnarly CL-accented research-quality prototype, but the result was surprisingly effective. Sadly, I never really managed to recover loops or function calls from the fully inlined trace, so even medium-size kernels would exhaust the instruction cache.

I believe I now see a practical and scalable solution, thanks to Artur Jez’s work on “A really simple approximation of smallest grammar.” His work might lead to a function-oriented analogue of trace compilation. Trace compilers are notoriously weak on recursion (recursive function calls don’t map well to loops), so it would be nifty to have an alternative that identifies functions rather than loops.

This makes me quip that “(Trace) Compilation is Compression.” We can see trace compilers as lazily unpacking traces from the source program, rewriting them a bit, and recompressing traces in an executable format. Admittedly, the analogy is a bit of a stretch for classical compilers: they are less aggressive in decompressing source code and directly translate from one compressed representation (a small source file may describe billions of execution paths) to another.

Anyway… this is extremely hypothetical and Jez’s work is fun independently of my weekend speculations.

How to fail with LZ77

Once we cast a program trace as a sequence of opcodes (perhaps without operands, to expose more redundancy), it’s obvious that reducing code size is “just” compression, and LZ-type algorithms quickly come to mind: they compress strings by referring to earlier substrings.

The heart of LZ77 is a loop that streams through the input sequence and finds the longest common subsequence earlier in the input. In practice, the search usually considers a fixed-size window; when I write LZ77 here, I instead refer to the theoretical approach with an unbounded search window. Repeated LCS searches on an unbounded window sounds slow, but, in sophisticated implementations, the bottleneck is sorting the input string to generate a suffix array.

I don’t feel like being sophisticated and will implement a quadratic-time LCS search.

(defun longest-subseq (seq start)
  "Find the longest subseq of seq[start...] that begins before start."
  (let ((best 1)
        (index nil))
    (dotimes (i start (values index best))
      (let ((length (mismatch seq seq :start1 i :start2 start
                                      :test #'equal)))
        (assert length)
        (decf length i)
        (when (> length best)
          (setf best length
                index i))))))

Some backreferences clearly look like function calls.

CL-USER> (longest-subseq "abab" 0)
NIL ; There is no match to the left of abab
1   ;                                  ^
CL-USER> (longest-subseq "abab" 2)
0   ; There is a match for the second ab, starting
2   ; at index 0 and spanning 2 characters.

It’s a bit surprising at first, but some also correspond to repeat loops.

CL-USER> (longest-subseq "abababa" 2)
0 ; There is a match for "ababa", starting
5 ; at index 0 and spanning 5 characters.

This last patch is strange because it’s self-referential. However, if we decompress character by character, its meaning becomes obvious: we replicate the substring in [0, 1] to generate exactly 5 characters. This is basically a loop; we can handle partial copies with, e.g., rotation and entering the middle of the loop (like Duff’s device).

Lempel and Ziv’s result tells us that we can look for references greedily in an unbounded window and obtain asymptotically optimal (proportional to the string’s entropy) compression. Again, there are algorithms to do that in linear time – via radix sort – but I’ll just bruteforce my way in cubic time.

(defstruct factor start length subseq)

(defun factorise (seq)
  (let ((index 0)
        (length (length seq)))
    (loop while (< index length)
          collect
          (multiple-value-bind (start length)
              (longest-subseq seq index)
            (prog1
                (if (null start)
                    (elt seq index)
                    (make-factor :start start :length length
                                 :subseq (subseq seq start (+ start length))))
              (incf index length))))))

Here’s the problem with converting an LZ77 factorisation into calls and loops: there is no guarantee that patches nest sanely.

CL-USER> (factorise "ababac||bac")
(#\a #\b #S(FACTOR :START 0 :LENGTH 3 :SUBSEQ "aba") #\c #\| #\|
 #S(FACTOR :START 3 :LENGTH 3 :SUBSEQ "bac"))

This factorisation encodes “ababac||bac” by repeating “ab” two and a half times, inserting “c||”, and then repeating “bac.” The issue is that we wish to convert “ababa” into a loop, but the last patch would then need to enter that loop in its last iteration. We could also have the opposite problem, with a patch that only covers a prefix of an earlier patch (a few iterations of a loop). The sketch below shows how we might even have to deal with both issues in the same factor.

Jez’s solution

Jez’s paper analyses a method to recover a CFL with a single member, the string we wish to compress. The CFL is described by a fully deterministic (it produces exactly one string) CFG in Chomsky normal form, i.e., a straight-line program.

This “really simple” approach takes a step back from LZ compression and instead starts with the easiest, greedy, way to generate a straight-line program from a string: just pair characters as you encounter them, left-to-right.

For example, on “abab,” this would pair “(ab)(ab)” and then “((ab)(ab)),” and generate the following grammar:

G -> XX
X -> ab

We got lucky: the repetition synced up with the greedy pairing. That’s not always the case; for example, “abcab” becomes “(ab)(ca)b” – which exposes no redundancy – rather than “(ab)c(ab).”

Jez addresses this issue by using LZ77 factorisation as an oracle to synchronise pairings.

First, we simplify the algorithm by assuming that there are no factors that begin exactly one character before their output. Such factors correspond to repetitions of that one character (e.g., “aaaa” = “a” x 4) and we can easily turn them into repetitions of a pair (e.g., “aa” x 2).

It’s then simply a matter of not pairing when it would prevent the next character from synchronising with its backreference. For example, in “abcab,” we’d skip pairing “ca” so that “ab” could pair like the first occurrence did. We also don’t force a pair when the backreference only includes the first letter, but not the second. Finally, we opportunistically match consecutive unpaired letters.

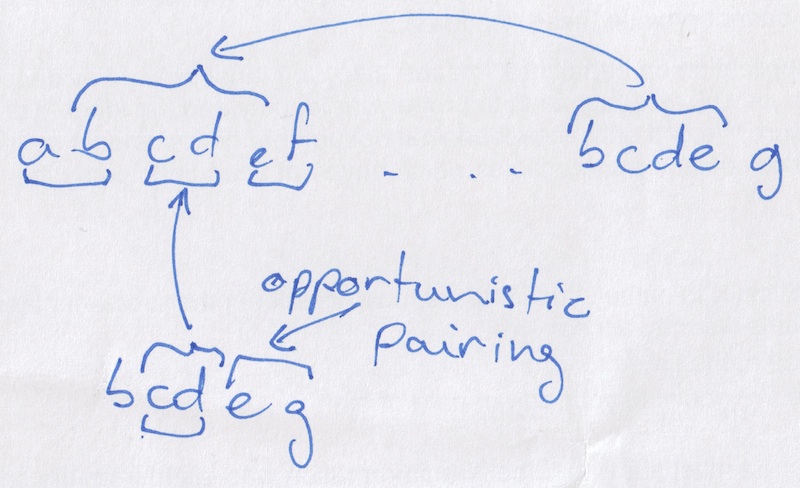
Each such pass creates a new, shorter, string of literals and production rules. We iteratively apply the guided pairing loop until we’re left with a single production rule.

That’s it. Jez’s paper is mostly concerned with showing that we only have to run LZ compression once and with proving suboptimality bounds. The key is that we can convert factors for the input into factors for the output, and that each pass shrinks the string by a multiplicative factor. I’ll simplify things further by recomputing a factorisation (in cubic time!) from scratch in each pass.

Now, the code

;; specials for shared state (quick-and-dirty REPL style)

;; For each character position, whether it's the first or
;; second of a pair, or just a singleton (nil)
(defvar *state*)
;; The sequence to compress.
(defvar *sequence*)
;; Cursor in the sequence.
(defvar *index*)

(defmacro with-sequence ((seq) &body body)
  (let ((temp (gensym "SEQ")))
    `(let* ((,temp ,seq)
            (*sequence* ,temp)
            (*state* (make-array (length *sequence*)
                                 :initial-element nil))
            (*index* 0))
       ,@body)))

;; No pair begins here, but we might still fuse with the previous
;; singleton.
(defun single ()
  (let ((i *index*))
    (when (and (plusp i)
               (null (aref *state* (1- i))))
      (setf (aref *state* (1- i)) 'first
            (aref *state* i) 'second)))
  (incf *index*))

;; Force a pair.
(defun pair ()
  (let ((i *index*))
    ;; we mustn't be at the end of the sequence
    (assert (< (1+ i) (length *sequence*)))
    (setf (aref *state* i) 'first)
    (setf (aref *state* (1+ i)) 'second)
    (incf *index* 2)))

(defun sync-and-pair ()
  (multiple-value-bind (begin length)
      (longest-subseq *sequence* *index*)
    (cond ((null begin)
           ;; No factor; advance and merge greedily.
           (single))
          ((= begin (1- *index*))
           ;; Single-character repetition.
           (loop repeat length do (single)))
          (t
           (let ((end (+ begin length)))
             (assert (<= end (length *sequence*)))
             (assert (< begin (1- *index*)))
             (when (eql 'second (aref *state* begin))
               ;; The first character is the second half of a pair;
               ;; leave it by itself.
               (single)
               (incf begin))
             ;; Mimic the pairing decisions of the backref.
             (loop with expected = (+ *index* (- end begin))
                   for i from begin below end
                   do (ecase (aref *state* i)
                        (second)
                        (first (if (= (1+ i) end) ; Last character
                                   (single)       ; can't force
                                   (pair)))       ; a pair.
                        ((nil) (single)))
                   finally (assert (= *index* expected))))))))

My implementation is exceedingly naïve and runs in cubic time in the worst case. With a lot more work, the bottleneck (LZ77 factorisation) runs at the speed of sort… but constructing a suffix array would only get in the way of this post. Let’s just see what pairing the code generates.

CL-USER> (with-sequence ("abcab")
           (loop while (< *index* (length *sequence*))
                 do (sync-and-pair)
                 finally (return *state*)))
#(FIRST SECOND NIL FIRST SECOND)
CL-USER> (with-sequence ("abababa")
           (loop while (< *index* (length *sequence*))
                 do (sync-and-pair)
                 finally (return *state*)))
#(FIRST SECOND FIRST SECOND FIRST SECOND NIL)
CL-USER> (with-sequence ("ababac||bac")
           (loop while (< *index* (length *sequence*))
                 do (sync-and-pair)
                 finally (return *state*)))
#(FIRST SECOND FIRST SECOND FIRST SECOND FIRST SECOND NIL FIRST SECOND)

In short, “abcab” becomes “(ab)c(ab)”, “abababa” “(ab)(ab)(ab)a”, and “ababac||bac” “(ab)(ab)(ac)(||)b(ac)”.

Programs from pairs

So far, we’ve only made pairing decisions. The next step is to translate them into production rules (i.e., functions), and to merge equivalent rules to actually save space.

(defvar *counter* 0)
(defvar *rules* (make-array 0 :adjustable t :fill-pointer 0))

(defstruct rule
  (id (incf *counter*))
  a b)

;; Hash-consing naturally merges equivalent rules.
(fare-memoization:define-memo-function rule (a b)
  (let ((rule (make-rule :a a :b b)))
    (vector-push-extend rule *rules*)
    rule))

(defun reset-rules ()
  (setf *counter* 0)
  ;; Sorry, this is ugly.
  (fare-memoization:unmemoize 'rule)
  (fare-memoization:memoize 'rule)
  (setf *rules* (make-array 0 :adjustable t :fill-pointer 0)))

(defun pair-cfg (sequence state)
  (loop with acc = '()
        for i upfrom 0
        for character across sequence
        for choice across state
        do (ecase choice
             (second)
             (first (push (rule character (aref sequence (1+ i)))
                          acc))
             ((nil) (push character acc)))
        finally (return (coerce (nreverse acc) 'simple-vector))))

(defun compress-1 (sequence)
 (with-sequence (sequence)
    (loop with length = (length sequence)
          while (< *index* length)
          do (sync-and-pair)
          finally (return (pair-cfg *sequence* *state*)))))

On the examples above, we find:

CL-USER> (reset-rules)
#()
CL-USER> (compress-1 "abcab")
#(#S(RULE :ID 1 :A #\a :B #\b) #\c #S(RULE :ID 1 :A #\a :B #\b))
CL-USER> (compress-1 "abababa")
#(#S(RULE :ID 1 :A #\a :B #\b) #S(RULE :ID 1 :A #\a :B #\b)
  #S(RULE :ID 1 :A #\a :B #\b) #\a)
CL-USER> (compress-1 "ababac||bac")
#(#S(RULE :ID 1 :A #\a :B #\b) #S(RULE :ID 1 :A #\a :B #\b)
  #S(RULE :ID 2 :A #\a :B #\c) #S(RULE :ID 3 :A #\| :B #\|) #\b
  #S(RULE :ID 2 :A #\a :B #\c))

We only have to pair production rules further until the sequence consists of a single rule (or literal).

(defun refactor (sequence)
  (if (<= (length sequence) 1)
      sequence
      (refactor (compress-1 sequence))))

CL-USER> (refactor "ababac||bac")
#(#S(RULE
     :ID 8
     :A #S(RULE
           :ID 7
           :A #S(RULE
                 :ID 4
                 :A #S(RULE :ID 1 :A #\a :B #\b)
                 :B #S(RULE :ID 1 :A #\a :B #\b))
           :B #S(RULE
                 :ID 5
                 :A #S(RULE :ID 2 :A #\a :B #\c)
                 :B #S(RULE :ID 3 :A #\| :B #\|)))
     :B #S(RULE :ID 6 :A #\b :B #S(RULE :ID 2 :A #\a :B #\c))))

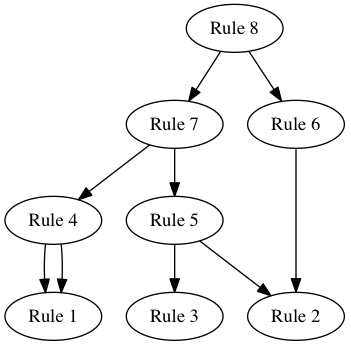
The “call graph” below shows there’s a lot of sharing for such a short string.

Enough with the strings

I started by writing about compiling program traces, but so far I’ve only been working with strings of characters. Let’s pretend the following PostScript file was written by someone who’s never heard of functions or loops.

%!PS
270 315 translate
1.5 setlinewidth

gsave
newpath
  0 36 moveto
 72 0  rlineto
  0 72 rlineto
-72 0  rlineto
closepath
stroke
grestore

45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore

showpage

Phew, programming is hard! That’s a lot of copy-paste to produce a simple pattern.

Let’s see what our (simplified) implementation of Jez’s algorithm can do.

CL-USER> (reset-rules)
#()
;; READ, the poor man's tokenizer.
CL-USER> (refactor #(
270 315 translate
1.5 setlinewidth

gsave
newpath
  0 36 moveto
 72 0  rlineto
  0 72 rlineto
-72 0  rlineto
closepath
stroke
grestore

45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore
45 rotate gsave newpath 0 36 moveto 72 0 rlineto 0 72 rlineto -72 0 rlineto closepath stroke grestore

showpage
))
#(#S(RULE
     :ID 35
   ...))

35 functions that each contain two literals or function calls. Not bad (: It’s an actual SMOP to convert this grammar into a PostScript program.

(defun emit-one-rule (stream rule)
  (flet ((emit-subrule (x)
           (if (rule-p x)
               (format nil "R~A" (rule-id x))
               (format nil "~(~a~)" x))))
    (format stream "/R~A { ~A ~A } def~%"
            (rule-id rule)
            (emit-subrule (rule-a rule))
            (emit-subrule (rule-b rule)))))

(defun emit-rules (stream rules)
  (map nil (lambda (rule)
             (emit-one-rule stream rule))
       rules)
  (format stream "R~A~%" (rule-id (elt rules (1- (length rules))))))

CL-USER> (emit-rules *standard-output* *rules*)
/R1 { 270 315 } def
/R2 { translate 1.5 } def
/R3 { setlinewidth gsave } def
/R4 { newpath 0 } def
/R5 { 36 moveto } def
/R6 { 72 0 } def
/R7 { rlineto 0 } def
/R8 { 72 rlineto } def
/R9 { -72 0 } def
/R10 { rlineto closepath } def
/R11 { stroke grestore } def
/R12 { 45 rotate } def
/R13 { R1 R2 } def
/R14 { R3 R4 } def
/R15 { R5 R6 } def
/R16 { R7 R8 } def
/R17 { R9 R10 } def
/R18 { R11 R12 } def
/R19 { gsave R4 } def
/R20 { R11 showpage } def
/R21 { R13 R14 } def
/R22 { R15 R16 } def
/R23 { R17 R18 } def
/R24 { R17 R20 } def
/R25 { R21 R22 } def
/R26 { R23 R19 } def
/R27 { R22 R24 } def
/R28 { R25 R26 } def
/R29 { R22 R26 } def
/R30 { R28 R29 } def
/R31 { R29 R29 } def
/R32 { R29 R27 } def
/R33 { R30 R31 } def
/R34 { R31 R32 } def
/R35 { R33 R34 } def
R35

This second PostScript program comprises 211 tokens, rather than the original’s 156, but 105 of those are “{ } def” noise to define functions. Arguably, the number of meaningful tokens was reduced from 156 to slightly more than 100. Crucially, the output remains the same.

Stack programs seem particularly well suited to this rewriting approach: explicit operands (e.g., registers) introduce trivial discrepancies. In a VM, I would consider “compressing” the opcode stream separately from the operands. Compiling only the former to native code would already reduce interpretative overhead, and extracting function calls from the instruction stream should avoid catastrophic size explosions.

There are several obvious deficiencies in the direct LZ77-guided pairing. Just breaking Chomsky normalisation to inline single-use function would already help. It might also make sense to special-case repetitions as repeat n loops, instead of hiding that in \(\log n\) levels of recursion. In a real program, it would also be useful to inline the bottom-most rules so as not to drown in control flow. The thing is, destroying structure in the name of performance is well understood compiler tech; recovering it efficiently was the hard part.

Paul Khuong: some Lisp

Refactoring with LZ77: compression is compilation (?)

How to fail with LZ77

Jez’s solution

Now, the code

Programs from pairs

Enough with the strings

Comments